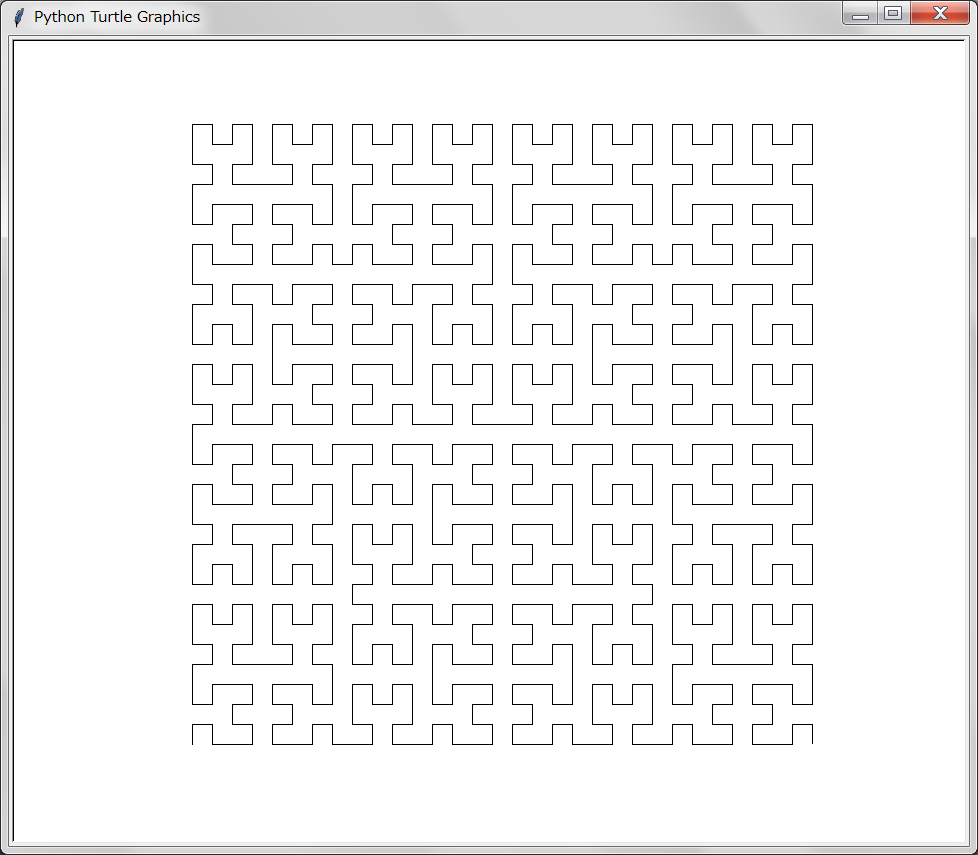
中華どんぶりに描かれているような「一筆書き」である。このような描画はPythonのタートル・グラフィックスが得意とするものである。「Turbo Graphics」(安齋利洋・伊吹龍著;1987年)に載っているPascal風のプログラムをなぞって作ったのが以下のものだ(元のプログラムにあったkameの大域変数は関数の引数とするようにした)。
#coding: utf-8
import myturtle
depth = 7 #再帰の深さ
atom = 3 #最小の長さ
def deko(kame, level):
if(level == 0):
return
else:
kame.reverse()
kame.rt(90)
deko(kame, level-1)
kame.reverse()
kame.fd(atom)
kame.rt(90)
deko(kame, level-1)
kame.fd(atom)
deko(kame, level-1)
kame.rt(90)
kame.fd(atom)
kame.reverse()
deko(kame,level-1)
kame.rt(90)
kame.reverse()
if __name__ == '__main__':
kame = myturtle.MyTurtle()
kame.ht()
kame.setposition(-300,-300)
kame.clear()
deko(kame, depth)
このプログラムでは二つの定数(depth, atom)が定義されているが、atomは描画が画面内に納まるようにするためのものである。定数depthは再帰の深さを示すものでこの曲線にとっては本質的なものである。
定数depthを大きくしたときの描画は実に奇妙である。以下depth=8の例を示す:
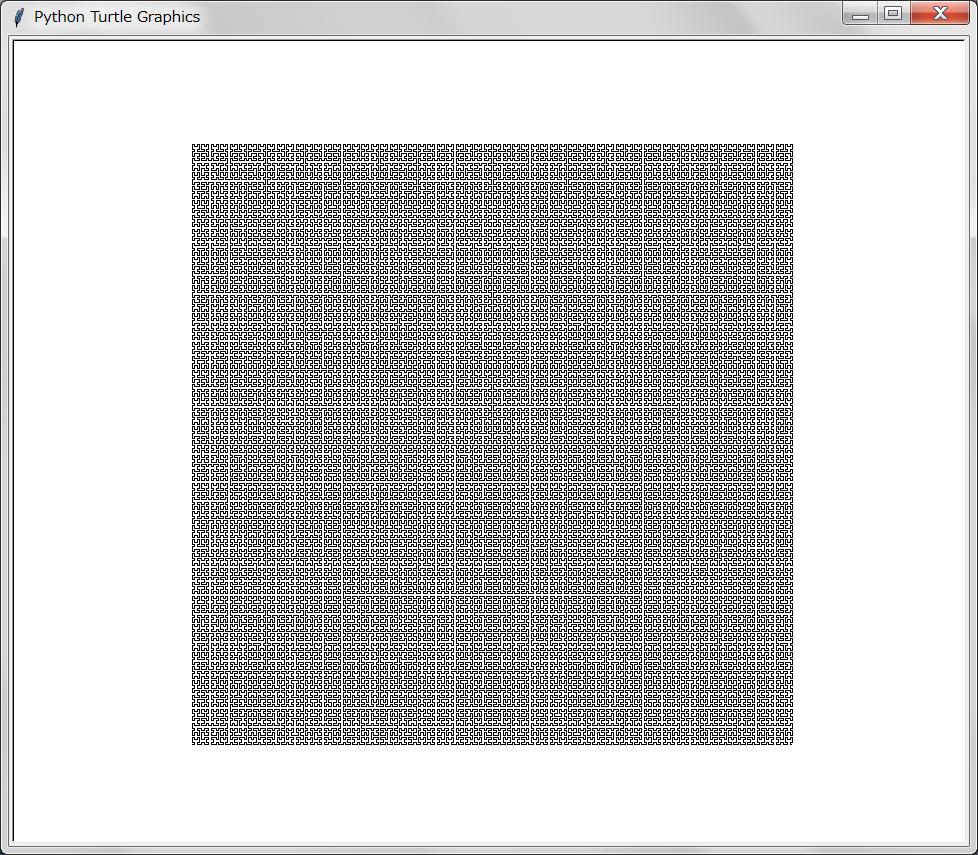
一本の線分(両端がある)にも拘わらず平面を埋め尽くすような描画ができる。再帰の深さ(depth)を無限大にする極限でこの線分は平面を文字通り埋め尽くして平面を作ることが知られている。
