投稿日:

Pythonのタートル・グラフィックス（７）：本物らしく木を描く

「Turbo Graphics」（安齋利洋・伊吹龍著；1987年）には本物らしく木を描画するプログラムが紹介されている。オリジナルのアルゴリズムは本田久夫氏（「樹木の分枝」別冊『数理科学』形・フラクタル、p78）との注がある。

プログラムは描画のためのパラメターをファイルから読み込むなど凝ったものになっているがここでは描画のエッセンスだけを抜き出しPythonで書いてみた：


#coding: utf-8

import myturtle

#パラメター
xP=0
yP=-300
angleMiki=15
ratioMiki = 0.80
angleEda=45
ratioEda=0.70
length=150
ratioFutosa=0.7200
generation=10


class Seed:
    """木の表現のためのパラメター類"""

def ki(tane):

    def edawakare(mikiT, length, thickness, depth):
        if(depth ==0 or length < 2 or thickness < 0.1):
            return
        miki=mikiT.clone()
        miki.reverse()
        miki.fd(length)
        eda=miki.clone()
        miki.lt(tane.angleMiki)
        edawakare(miki, length*tane.ratioMiki, thickness, depth-1)
        eda.rt(tane.angleEda)
        edawakare(eda, length*tane.ratioEda, thickness*tane.ratioFutosa, \
                  depth-1)
        
    miki=myturtle.MyTurtle()
    miki.ht()
    miki.lt(90)
    miki.setposition(tane.xP, tane.yP)
    miki.clear()
    edawakare(miki, tane.length, 1, tane.generation)

if __name__ == '__main__':

    tane=Seed()
    tane.xP=xP
    tane.yP=yP
    tane.angleMiki=angleMiki
    tane.ratioMiki=ratioMiki
    tane.angleEda=angleEda
    tane.ratioEda=ratioEda
    tane.length=length
    tane.ratioFutosa=ratioFutosa
    tane.generation=generation
    
        
    ki( tane)

ここでは関数内ではクローンturtleを使っている。

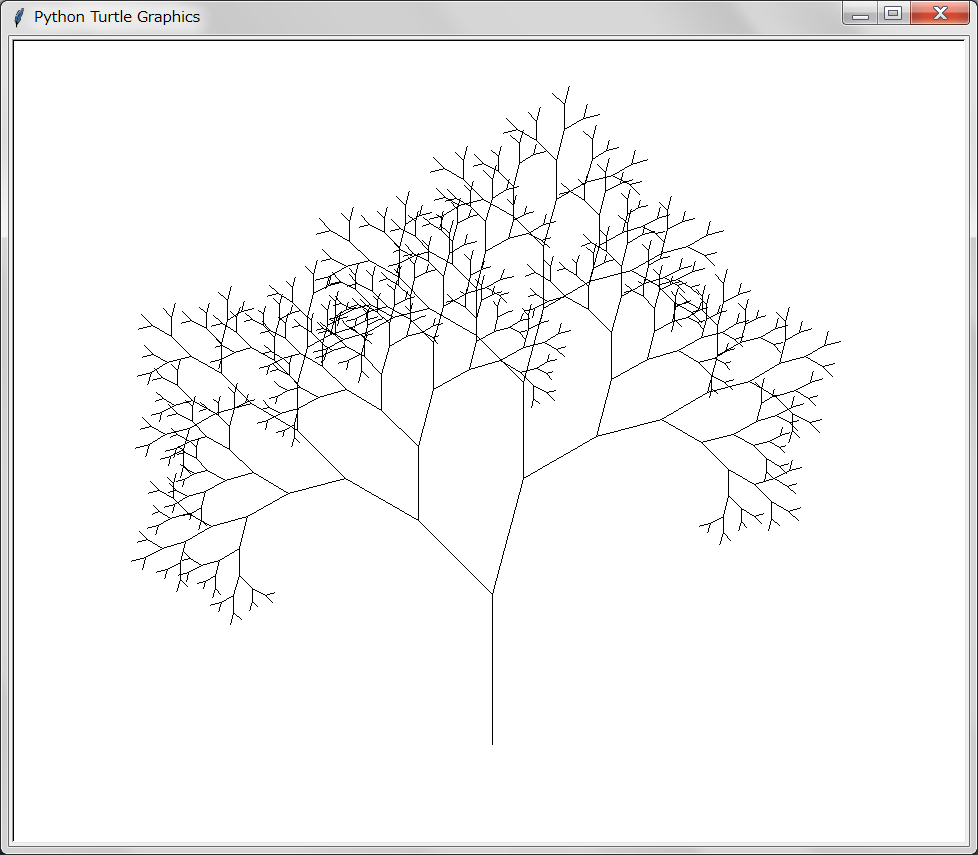
【実行結果の描画】

タートル・グラフィックスによる木
投稿日:

Pythonのタートル・グラフィックス（６）：木を描く

MYTurtleクラスを使って木を描くことにする。プログラムは以下のようになる：


import myturtle



angle = 60
ratio = 0.5
def ki( mikiT, length):
    if( length > 1):
        miki=mikiT.clone()
        miki.reverse()
        miki.fd(length)
        ki(miki, ratio*length)
        miki.rt(angle)
        ki(miki, ratio*length)
     

if __name__ == '__main__':
    
        
    miki = myturtle.MyTurtle()
    miki.clear()
    miki.ht()
    miki.lt(90)
    miki.setposition(0,-200)
    ki( miki, 200)

ここでは関数kiの引数に入るturtleオブジェクトがこのki関数で変化しないようにturtleオブジェクトのクローンを作って描画させている。

このクローンを使わない方法をとるにはki関数内でダミーな動きをさせて結果的にturtleオブジェクトの状態変化がなかったようにする：


import myturtle



angle = 60
ratio = 0.5
def ki( miki, length):
    if( length > 1):
        miki.reverse()
        miki.fd(length)
        ki(miki, ratio*length)
        miki.rt(angle)
        ki(miki, ratio*length)
        miki.lt(angle) #ダミー
        miki.bk(length) #ダミー
        miki.reverse() #ダミー
    

if __name__ == '__main__':
    
        
    miki = myturtle.MyTurtle()
    miki.clear()
    miki.ht()
    miki.lt(90)
    miki.setposition(0,-200)
    ki( miki, 200)

【描画の結果】

クローンkiなしのki
投稿日:

Pythonのタートル・グラフィックス（５）：MyTurtleクラスの導入

「Turbo Graphics」（安齋利洋・伊吹龍著；1987年）にはタートルの動きに対する面白い命令がある。それがreverseである。これはタートルの右回転（rt）と左回転（lt）の役割を反転させる機能を持っている。Pythonのタートル・グラフィックスにはこの機能がない。Python上でこの機能を関数として定義してもよいが折角なのでreverseをタートルクラスの一つメソッドとして追加したMyTurtleクラスを作ることにする。

MyTurtleクラスは元々のモジュール（turtle）で定義されているTurtleクラスを継承して作る。クラスの定義は以下のようなものである：


import turtle

class MyTurtle(turtle.Turtle):
    def __init__(self):
        turtle.Turtle.__init__(self)
        self.phase = 1

    def rt(self, angle):
        self.angle = angle*self.phase
        turtle.Turtle.rt(self, self.angle)

    def lt(self, angle):
        self.angle = angle*self.phase
        turtle.Turtle.lt(self, self.angle)

    def rev(self):
        return self.phase

    def reverse(self):
        self.phase=self.phase*-1

    def clone(self):
        temp=turtle.Turtle.clone(self)
        temp.phase = self.phase
        return temp

このクラスではreverseの導入によって影響を受けるturtleモジュールの中のメッソドの書き換えは最小限に止めてある。