稲の起源に触れて「栽培植物と農耕に起源」（中尾佐助著）の中で述べられている語句である。
アフリカやインドのサバンナ農耕文化は雑穀の文化である。このサバンナ農耕文化でも夏のモンスーン雨期には禾本科の草の穀物を採取して食料としていた。この周辺の雨の多い地帯で食料とされた湿生の雑穀の一つがイネであった。それは西アフリカとインド東部を起源とする。
輪王寺の撮影会（2021.10.27）
Pythonのタートル・グラフィックス（１０）：canvasに木を描く
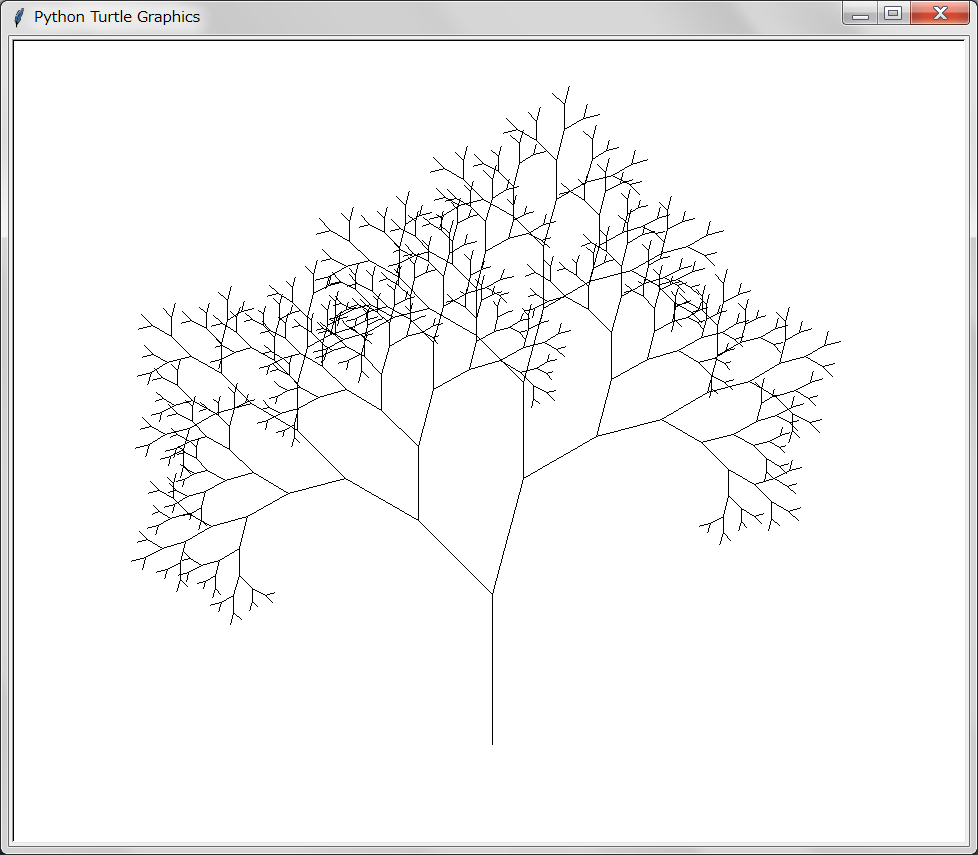
Pythonのタートル・グラフィックスはTkinterを基礎に作られているのでTkinterのcanvasウィジェット上にタートル・グラフィックスで描画を行うことは容易である。しかもTkinterのメニューなどの他のウィジェットも画面構成に使える。ここでは本物らしく木を描くタートル・グラフィックスをcanvas上で実行し、入力パラメタをentryウィジェットを使って入力するようにする。サンプル画像を以下に示す：
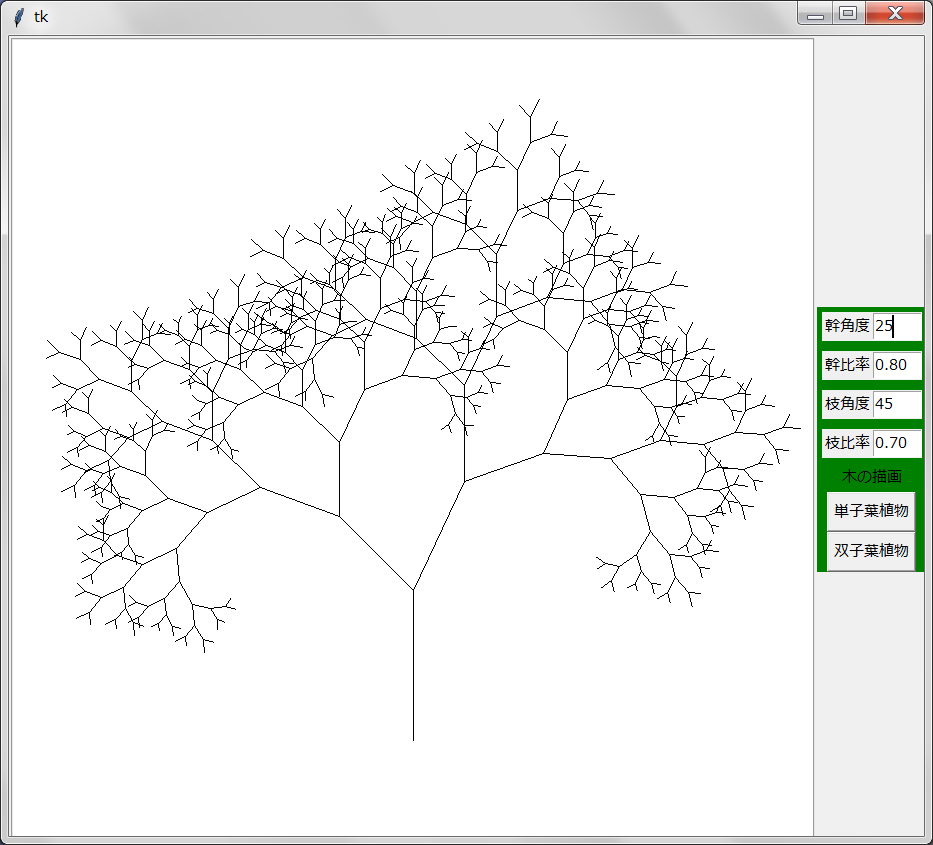
左側がcanvasで、右側がentryを含むメニューである。「Turbo Graphics」（安齋利洋・伊吹龍著；1987年）では二種類（単子葉植物、双子葉植物）の木の描画アルゴリズムが載っているがここではメニューで種類を選べるようにしてある。
Pythonのプログラムはここにある。
Pythonのタートル・グラフィックス（９）：ヒルベルト（Hirbert）曲線を描く
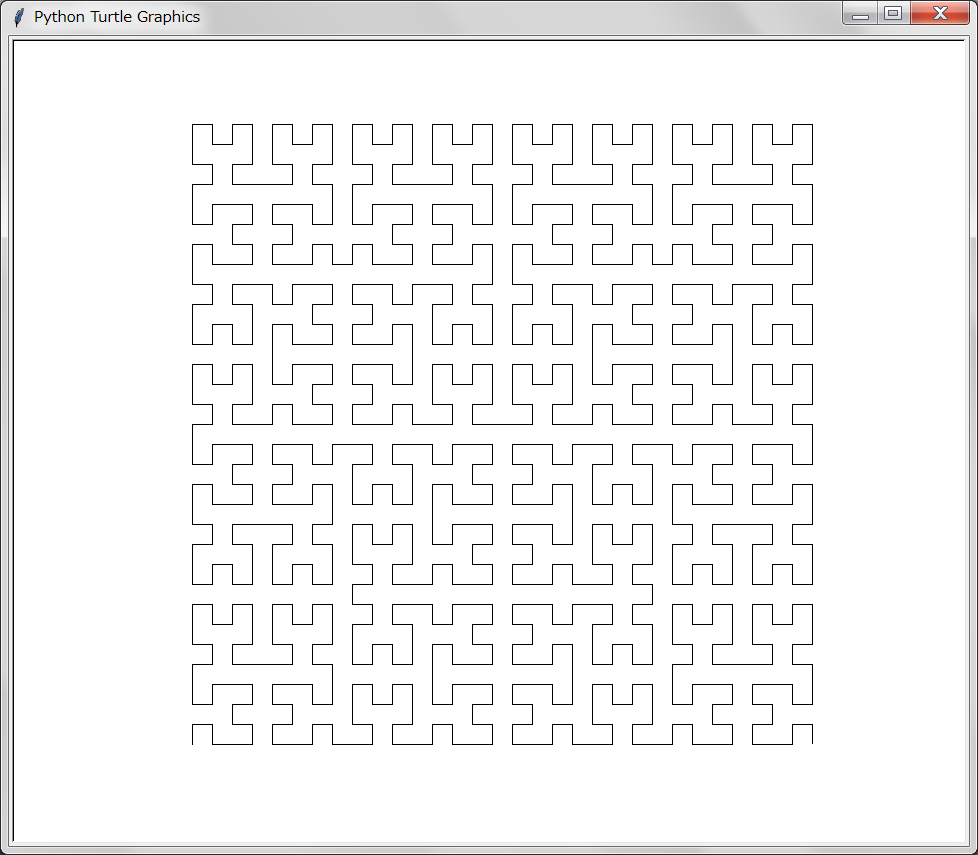
中華どんぶりに描かれているような「一筆書き」である。このような描画はPythonのタートル・グラフィックスが得意とするものである。「Turbo Graphics」（安齋利洋・伊吹龍著；1987年）に載っているPascal風のプログラムをなぞって作ったのが以下のものだ（元のプログラムにあったkameの大域変数は関数の引数とするようにした）。
#coding: utf-8
import myturtle
depth = 7 #再帰の深さ
atom = 3 #最小の長さ
def deko(kame, level):
if(level == 0):
return
else:
kame.reverse()
kame.rt(90)
deko(kame, level-1)
kame.reverse()
kame.fd(atom)
kame.rt(90)
deko(kame, level-1)
kame.fd(atom)
deko(kame, level-1)
kame.rt(90)
kame.fd(atom)
kame.reverse()
deko(kame,level-1)
kame.rt(90)
kame.reverse()
if __name__ == '__main__':
kame = myturtle.MyTurtle()
kame.ht()
kame.setposition(-300,-300)
kame.clear()
deko(kame, depth)
このプログラムでは二つの定数（depth, atom）が定義されているが、atomは描画が画面内に納まるようにするためのものである。定数depthは再帰の深さを示すものでこの曲線にとっては本質的なものである。
定数depthを大きくしたときの描画は実に奇妙である。以下depth=8の例を示す：
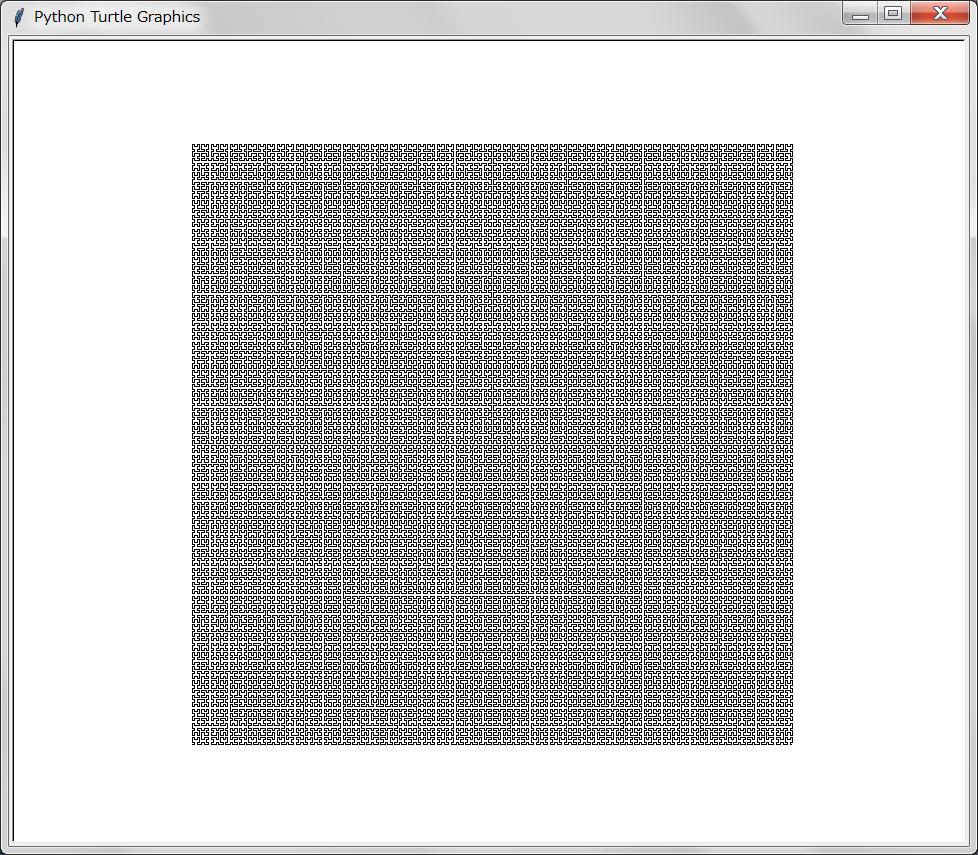
一本の線分（両端がある）にも拘わらず平面を埋め尽くすような描画ができる。再帰の深さ（depth）を無限大にする極限でこの線分は平面を文字通り埋め尽くして平面を作ることが知られている。
Pythonのタートル・グラフィックス（８）：コッホ（Koch）曲線を描く
有名なコッホ（Koch）曲線を描く。「Turbo Graphics」（安齋利洋・伊吹龍著；1987年）に載っているPascal風のプログラムをなぞって作ったのが以下のものだ：
#coding: utf-8
import myturtle
depth = 5 #再帰の深さ
def koch(length, level):
global kame
if(level > 0):
len1 = length /3
koch(len1, level-1)
kame.lt(60)
koch(len1, level-1)
kame.rt(120)
koch(len1, level-1)
kame.lt(60)
koch(len1, level-1)
else:
kame.fd(length)
if __name__ == '__main__':
kame = myturtle.MyTurtle()
kame.ht()
kame.setposition(-320,-0)
kame.clear()
koch(640, depth)
【描画】
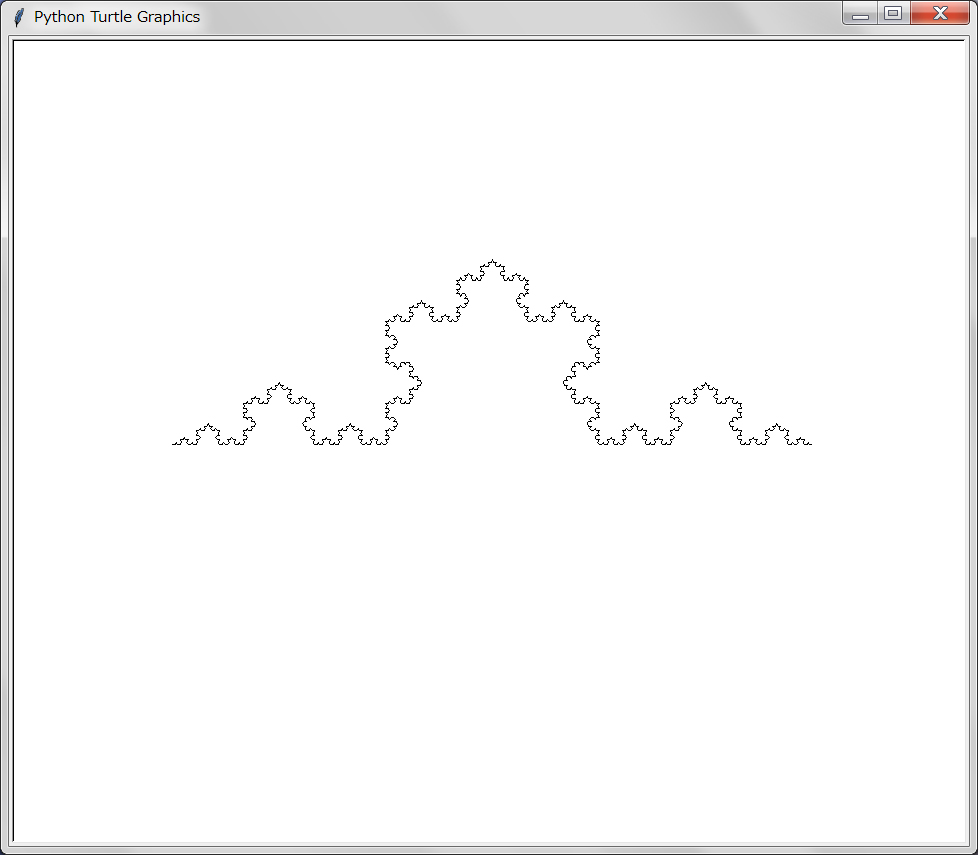
複雑であるが折れ線による「一筆描き」である。このような「一筆描き」ではあるセグメントの折れ線ではこれまで描かれた折れ線の先端を起点として一つの折れ線を描き、その折れ線の先端は次の折れ線の起点となるような処理が必要となる。上のプログラムではこれをkameを大域変数（global）とすることで行っている。こうすることでkameが折れ線を描く毎にkameの属性（位置）が更新される。
このような事情を考慮して直接Pythonで書くと以下のようになる：
#coding: utf-8
import myturtle
depth = 5 #再帰の深さ
def koch(kame, length, level):
if(level > 0):
len1 = length /3
koch(kame, len1, level-1)
kame.lt(60)
koch(kame, len1, level-1)
kame.rt(120)
koch(kame, len1, level-1)
kame.lt(60)
koch(kame, len1, level-1)
else:
kame.fd(length)
if __name__ == '__main__':
kame = myturtle.MyTurtle()
kame.ht()
kame.setposition(-320,-0)
kame.clear()
koch(kame, 640, depth)
このプログラムではkameは関数kochの引数の一つとして関数kochに渡されるようになっている。このプログラムはPascal風の処理系では期待通りの結果は得られないが、Pythonでは上の描画と同じものが得られる。Pythonでは関数に渡されたオブジェクトkameは関数内の変更を受けて実引数のkameの属性も変更されるからだ。
Pythonではkameを大域変数とするプログラムも、kameを関数の引数として渡すプログラムも作れる。後者は少しトリッキーな気もするが。
Pythonのタートル・グラフィックス（７）：本物らしく木を描く
「Turbo Graphics」（安齋利洋・伊吹龍著；1987年）には本物らしく木を描画するプログラムが紹介されている。オリジナルのアルゴリズムは本田久夫氏（「樹木の分枝」別冊『数理科学』形・フラクタル、p78）との注がある。
プログラムは描画のためのパラメターをファイルから読み込むなど凝ったものになっているがここでは描画のエッセンスだけを抜き出しPythonで書いてみた：
#coding: utf-8
import myturtle
#パラメター
xP=0
yP=-300
angleMiki=15
ratioMiki = 0.80
angleEda=45
ratioEda=0.70
length=150
ratioFutosa=0.7200
generation=10
class Seed:
"""木の表現のためのパラメター類"""
def ki(tane):
def edawakare(mikiT, length, thickness, depth):
if(depth ==0 or length < 2 or thickness < 0.1):
return
miki=mikiT.clone()
miki.reverse()
miki.fd(length)
eda=miki.clone()
miki.lt(tane.angleMiki)
edawakare(miki, length*tane.ratioMiki, thickness, depth-1)
eda.rt(tane.angleEda)
edawakare(eda, length*tane.ratioEda, thickness*tane.ratioFutosa, \
depth-1)
miki=myturtle.MyTurtle()
miki.ht()
miki.lt(90)
miki.setposition(tane.xP, tane.yP)
miki.clear()
edawakare(miki, tane.length, 1, tane.generation)
if __name__ == '__main__':
tane=Seed()
tane.xP=xP
tane.yP=yP
tane.angleMiki=angleMiki
tane.ratioMiki=ratioMiki
tane.angleEda=angleEda
tane.ratioEda=ratioEda
tane.length=length
tane.ratioFutosa=ratioFutosa
tane.generation=generation
ki( tane)
ここでは関数内ではクローンturtleを使っている。
【実行結果の描画】
Pythonのタートル・グラフィックス（６）：木を描く
MYTurtleクラスを使って木を描くことにする。プログラムは以下のようになる：
import myturtle
angle = 60
ratio = 0.5
def ki( mikiT, length):
if( length > 1):
miki=mikiT.clone()
miki.reverse()
miki.fd(length)
ki(miki, ratio*length)
miki.rt(angle)
ki(miki, ratio*length)
if __name__ == '__main__':
miki = myturtle.MyTurtle()
miki.clear()
miki.ht()
miki.lt(90)
miki.setposition(0,-200)
ki( miki, 200)
ここでは関数kiの引数に入るturtleオブジェクトがこのki関数で変化しないようにturtleオブジェクトのクローンを作って描画させている。
このクローンを使わない方法をとるにはki関数内でダミーな動きをさせて結果的にturtleオブジェクトの状態変化がなかったようにする：
import myturtle
angle = 60
ratio = 0.5
def ki( miki, length):
if( length > 1):
miki.reverse()
miki.fd(length)
ki(miki, ratio*length)
miki.rt(angle)
ki(miki, ratio*length)
miki.lt(angle) #ダミー
miki.bk(length) #ダミー
miki.reverse() #ダミー
if __name__ == '__main__':
miki = myturtle.MyTurtle()
miki.clear()
miki.ht()
miki.lt(90)
miki.setposition(0,-200)
ki( miki, 200)
【描画の結果】
Pythonのタートル・グラフィックス（５）：MyTurtleクラスの導入
「Turbo Graphics」（安齋利洋・伊吹龍著；1987年）にはタートルの動きに対する面白い命令がある。それがreverseである。これはタートルの右回転（rt）と左回転（lt）の役割を反転させる機能を持っている。Pythonのタートル・グラフィックスにはこの機能がない。Python上でこの機能を関数として定義してもよいが折角なのでreverseをタートルクラスの一つメソッドとして追加したMyTurtleクラスを作ることにする。
MyTurtleクラスは元々のモジュール（turtle）で定義されているTurtleクラスを継承して作る。クラスの定義は以下のようなものである：
import turtle
class MyTurtle(turtle.Turtle):
def __init__(self):
turtle.Turtle.__init__(self)
self.phase = 1
def rt(self, angle):
self.angle = angle*self.phase
turtle.Turtle.rt(self, self.angle)
def lt(self, angle):
self.angle = angle*self.phase
turtle.Turtle.lt(self, self.angle)
def rev(self):
return self.phase
def reverse(self):
self.phase=self.phase*-1
def clone(self):
temp=turtle.Turtle.clone(self)
temp.phase = self.phase
return temp
このクラスではreverseの導入によって影響を受けるturtleモジュールの中のメッソドの書き換えは最小限に止めてある。
地球の気候変動と非線形性
世界的な規模で地球の気候変動が問題になっている。人間活動がこの変動に深く関わっているからだ。
地球の気候の変動は様々な要因で起こる。地球に対する太陽の影響の変化、地球内部の活動の変化と言った自然要因もある。勿論人間活動もその一つである。気候変動の特徴は非線形性にあると思う。
非線形性が強い現象にカオスがある。これを初めて見つけた気象学者のローレンツはこの現象を「バタフライ効果」と呼んだ。何処かで蝶がする一振りの羽ばたきが何処かで竜巻を起こす原因になる。
身近な例でカオスを説明しようとすると「パイこね」がある。パイの生地を捏ねるには生地を伸ばして重ねるという作業を繰り返す。このパイの生地に二つの砂糖の粒を隣接して置いておく。このパイ捏ねの作業を続けていると隣接した砂糖粒は見る間に離れて行き過去に隣接していたとは思えないような振る舞いする。これがカオスである。
この砂糖粒の一つが自然要因だけの地球の気候で、隣接する砂糖粒が人間活動を伴なった地球の気候と考えてみよう。僅かにことなるだけである。しかし時間が経つと二つは似てもつかない振る舞いをする。これが地球の気候だ。
「これくらいは僅かなので大丈夫」という考えは将来もその差が僅かであると予断している。これを「線形思考」という。しかし地球の気候変動が強い非線形性を持っているとしたら、「線形思考」ではなく、「非線形思考」が必要になる。
バナナは人類が最古に改良した種無し果実
「栽培植物と農耕の起源」（中尾佐助著）によれば、今、日常に食しているバナナは人類が種ありの野生バナナを改良して種無しバナナにしたものだ。その改良が行われたのは今から5000年も前のことだ。
野生のバナナは学名をムサ・アクミタータ（Musa acuminata）と言う。大きな果実だが中にはアズキ粒ぐらいの種がぎっしりと入っている。
「栽培植物と農耕の起源」（中尾佐助著）にはこれを種無しにしたプロセスが詳しく述べられている。このプロセスは長い時間が必要だった。