LibreOfficeのマクロをPythonで書くことを調べてきたが、この付録ではほんの少しだけ実用的になるかなというマクロの話である。
Calcのシートにデータを入力(例えば住所録)するときにはプルダウン・メニュの「ツール」->「フォーム」を選ぶと入力窓が出てきて入力ができる。しかしこれでも機械的だと思われる。
そこでベタ書き用の入力窓が出てきて適当に住所をベタ書きするとそれをシートに転写してくれるようなマクロを作ってみた。
【マクロ】
#coding: utf-8
import uno
import screen_io as ui
import unohelper
from com.sun.star.awt import XKeyListener
class MyKeyListener(unohelper.Base, XKeyListener):
def __init__(self, sheet, textf1):
self.sheet = sheet
self.textf1 = textf1
self.row = 0
def keyPressed( self, event ):
k = event.KeyCode
c = event.KeyChar.value
mods = event.Modifiers
# mods are additive
# 0 - None
# 1 - Shift
# 2 - Ctrl
# 4 - Alt
# 8 - Super_R
print(k, c, mods)
if k == 1282: #キー
#表への書き出し
self.row+=1
print(self.row)
textd = self.textf1.Text
print(textd)
sheetd=textd.split("\n")
print(len(sheetd))
for i, celld in enumerate(sheetd):
self.sheet.getCellByPosition(i,self.row).String=celld
self.textf1.Text = ''
def createDialog(*args):
ctx = XSCRIPTCONTEXT.getComponentContext()
smgr = ctx.getServiceManager()
dp = smgr.createInstanceWithContext("com.sun.star.awt.DialogProvider", ctx)
dialog = dp.createDialog("vnd.sun.star.script:Standard.Dialog5?location=application")
#表
doc = XSCRIPTCONTEXT.getDocument()
sheet = doc.Sheets[0]
#コントロールの登録
textf1 = dialog.getControl("TextField1")
#エヴェント監視(Enterキーを検出)
textf1_listener = MyKeyListener(sheet, textf1)
textf1.addKeyListener(textf1_listener)
dialog.execute()
dialog.dispose()
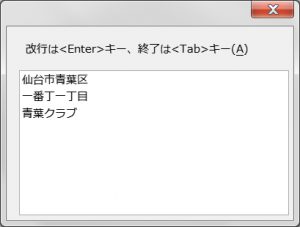 文字入力窓を持つダイアログ
文字入力窓を持つダイアログ
このマクロでは1つの入力の終わりはキーで行ったが、マウスをその窓に入れると終わりとするヴァージョンも作ってみた。
【マクロ】
#coding: utf-8
import uno
import screen_io as ui
import unohelper
from com.sun.star.awt import XMouseListener
class MyMouseListener(unohelper.Base, XMouseListener):
def __init__(self, sheet, textf1):
self.sheet = sheet
self.textf1 = textf1
self.row = 0
def mouseEntered( self, event ):
#表への書き出し
self.row+=1
print(self.row)
textd = self.textf1.Text
print(textd)
sheetd=textd.split("\n")
print(len(sheetd))
for i, celld in enumerate(sheetd):
self.sheet.getCellByPosition(i,self.row).String=celld
self.textf1.Text = ''
return False
def mouseExited(self, event):
return False
def mousePressed(self, event):
return False
def mouseReleased(self, event):
return False
def createDialog(*args):
ctx = XSCRIPTCONTEXT.getComponentContext()
smgr = ctx.getServiceManager()
dp = smgr.createInstanceWithContext("com.sun.star.awt.DialogProvider", ctx)
dialog = dp.createDialog("vnd.sun.star.script:Standard.Dialog5?location=application")
#表
doc = XSCRIPTCONTEXT.getDocument()
sheet = doc.Sheets[0]
#コントロールの登録
textf1 = dialog.getControl("TextField1")
#エヴェント監視(Enterキーを検出)
textf1_listener = MyMouseListener(sheet, textf1)
textf1.addMouseListener(textf1_listener)
dialog.execute()
dialog.dispose()
この例では意図しないタイミングでマウスを窓に入れてしまうのでインタフェースとしてはオリジナルのものがよいと思われる。












